1. INCERTIDUMBRE Y AZAR
El ser humano primitivo poseía un muy limitado control sobre las condiciones ambientales, colocándolo en una situación de gran vulnerabilidad frente al medio que lo rodeaba. Es posible imaginar su estupor frente a ciertos eventos climáticos, como tormentas eléctricas, o ante fenómenos telúricos o erupciones volcánicas. Frente a esta situación de indefensión, es razonable que buscara algún mecanismo que le permitiera obtener certezas, aunque estas fueran parciales. De esta forma, de manera natural buscará explicaciones de lo que observa aludiendo la intervención de fuerzas ocultas y superiores a él. Se inicia de esta forma la religión. Por lo tanto, el primer encuentro de la humanidad con el azar es a través de la incertidumbre frente a la naturaleza y su primera respuesta para dominarlo es la religión. Este será el inicio de un eterno conflicto del ser humano contra el azar.
La observación de fenómenos regulares y periódicos va incrementando su confianza en determinadas certezas, por ejemplo el amanecer de cada mañana o los ciclos de la luna; sin embargo, otros fenómenos continuarán en el ámbito de lo impredecible. Con el pasar de los siglos, y al iniciarse las civilizaciones, la humanidad irá creando complejos sistemas ideológicos para obtener el favor de los dioses y asegurar condiciones favorables para su subsistencia, entonces el azar entrará en otro ámbito de la vida, en el cual aún permanece.
2. LOS JUEGOS Y LAS APUESTAS
El nombre del juego
Los antecedentes más antiguos de juegos de azar provienen de la cultura sumeria y consistían en el lanzamiento de trozos de huesos (astrágalo) obtenidos del talón de algunos animales (Vega-Amaya, 2002). Este juego es el antecesor del dado, el cual es el juego de azar por antonomasia.
El origen de la palabra dado no es claro. Hay, al menos, dos hipótesis acerca de su procedencia: la primera que provenga del latín datum de donde viene el verbo dar; la segunda que provenga de árabe clásico a’dad, que significa números.
Imagen 1. Dados y fichas de hueso de época imperial romana

Fuente: Museo Caldoval, 2022.
En árabe clásico, el juego de los dados se denominaba azahar, de donde proviene la palabra azar. En la Roma clásica el juego del dado se denominaba alea, de donde proviene la palabra aleatorio.
Pero no solo en Europa y Medio Oriente se jugaba a la suerte. En Mesoamérica, la cultura teotihuacán jugaba patolli (Swezey y Bittman, 1983), mil años antes de Cristo y en tiempos del imperio inca se usaban dados de forma piramidal, denominados pichca (Gentile, 1998).
Imagen 2. Pichca
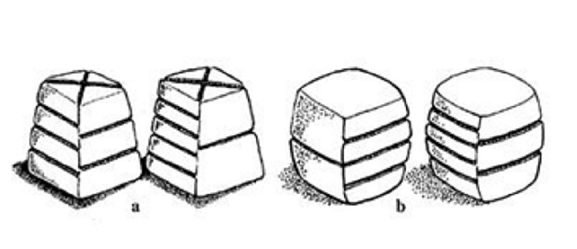
Fuente: Taboada, 2014.
La forma piramidal del dado inca muestra que no es obligatorio que un dado tenga forma cúbica. Desde la antigüedad que existen dados de variadas formas, casi siempre de poliedros regulares. Actualmente los juegos de rol han popularizado dados de una gran cantidad de caras. Por ejemplo, un dado extremal, es uno de cien caras.
Imagen 3. Zocchiedro o dado de cien caras

Fuente: Wikipedia, 2006.
Algunas preguntas interesantes: el hectaedro no es regular, ¿significa eso que los números pueden tener distintas probabilidades de ocurrencia?; si se usan dos dados de diez caras, ¿es equivalente a uno de cien caras?
3. PRIMERAS REFLEXIONES SOBRE EL AZAR Y SU NATURALEZA EN LA GRECIA CLÁSICA
• Los atomistas: para la escuela atomista griega todo lo real está formado por átomos y por el vacío donde se mueven los átomos. Los choques, agregaciones y disgregaciones de los átomos generan toda la realidad existente en un movimiento eterno (Rodríguez-Donís, 1997).
• El determinismo de Demócrito: para Demócrito el estado actual de las cosas determina el estado posterior de estas, por lo tanto es partidario de una visión mecanicista del universo.
La noción de azar puede mantenerse y usarse en un sentido restringido para indicar una causa que es y tiene que seguir siendo oscura para nosotros.
• El indeterminismo de Epicuro: para Epicuro los átomos pueden sufrir desviaciones aleatorias en sus trayectorias sin ninguna causa que las produzca. Con esto, se modifica la cadena causal y aseguraría la emergencia de la novedad y la libertad individual. Dante le dedicará en la Divina Comedia unos versos en el sexto círculo de su Infierno: “Su cementerio en esta parte tienen con Epicuro todos sus secuaces que el alma, dicen, con el cuerpo muere”.
Los pensamientos de Demócrito y Epicuro son conocidos gracias al poeta y filósofo atomista romano Tito Lucrecio Caro, quien los expuso en su obra De rerum natura (Sobre la naturaleza de las cosas).
• Aristóteles y la teoría causal: Aristóteles distinguía el ser en acto y el ser en potencia y el movimiento se entiende como la transformación del ser en potencia, en ser en acto. Esta transformación se produce por cuatro causas:
a) La causa material, la sustancia de lo que están hecha las cosas.
b) La causa formal, constituye la esencia como forma de la sustancia.
c) La causa eficiente, agente que produce el movimiento.
d) La causa final, que dirige el movimiento hacia un fin.
• El azar en Aristóteles: para Aristóteles el azar es cuando un determinado resultado ocurre en discordancia con las causas que debieran producirlo. Más precisamente, cual el resultado obtenido es distinto del fin esperado. Esta es una diferencia radical con la escuela atomista, la cual no reconoce la existencia de una causa primera ni una causa final (Rossi, 2013).
En este punto se pueden distinguir dos tipos de azar:
• Azar epistemológico: producto del nivel de conocimiento o información sobre las causas que producen determinando fenómeno.
• Azar ontológico: es aquel que no es reducible al nivel de conocimiento o información sobre el fenómeno. Se podría decir que es un azar en sí mismo o un azar puro (Delmastro et al., 2004).
La existencia de un auténtico azar ontológico aún es motivo de acalorados debates en los ámbitos filosófico y científico.
4. LA MATEMÁTICA HACE SU APARICIÓN EN EL DEBATE
En la discusión accidental, hasta la Edad Media, se centró exclusivamente en los aspectos conceptuales y filosóficos del azar, no existiendo una aproximación matemática a este. La mirada matemática sobre los fenómenos aleatorios requirió de la introducción de una idea del todo innovadora, asignar una medida a la ocurrencia de un determinado evento al azar, es decir, una probabilidad.
Con el concepto de probabilidad, la matemática hace su introducción en la problemática de los fenómenos aleatorios.
En Occidente, esto comenzó solo terminada la Edad Media, con la obra Liber de ludo aleae, escrita en la década de 1560 por el matemático italiano Gerolamo Cardano pero publicada en 1663. Posteriormente, Galileo Galilei (1564-1642) abordó los mismos problemas de Cardano en el libro Sopra le Scoperte dei Dadi, obra publicada recién en 1718.
¿Cuáles fueron las grandes ideas establecidas por Cardano y Galileo en sus trabajos? (Vega-Amaya, 2002). En lenguaje moderno se pueden escribir:
• Sea Ω={x1, x2, . . . , xn} los posibles resultados de un determinado fenómeno aleatorio.
• Cada posible resultado es equiprobable, es decir IP[xi]=1/n , ∀i = 1, . . . , n.
• Para A⊂Ω.
Puede parecer muy simple, como para clasificarlo como una gran aporte, sin embargo, importantes matemáticos se equivocaron en dar respuestas a temas relacionados con esta estructura, entre ellos Tartaglia, Leibniz y d’Alembert.
5. UN JUEGO INCONCLUSO CAMBIÓ LA HISTORIA
El problema de cómo repartir el fondo de una apuesta entre dos jugadores cuando esta se interrumpe, motivó grandes discusiones y variados intentos de respuesta. El problema ya aparece en un manuscrito italiano del año 1380, pero se cree que es una traducción de un texto árabe.
El problema de los puntos
Supongamos que dos jugadores apuestan 600 monedas cada uno, al primero que obtenga diez puntos en lanzamientos de cara y sello. Cuando el primero de ellos ha obtenido siete puntos y el segundo cinco, el juego se interrumpe. ¿Qué fracción de la cantidad de monedas le corresponde a cada uno?
Algunas propuestas de solución:
• Luca Pacioli (1445-1517) propuso dividir la apuesta en proporción al número de lanzamientos ganados por cada jugador. De esta forma, el primero obtiene 7/12 · 1200 = 700 y el segundo 5/12 · 1200 = 500.
• Tartaglia (1500-1557) propuso la división del premio en la proporción entre la medida de la ventaja y la longitud del juego. Es decir: el primero obtiene (7−5)/10 · 600 + 600 = 720 y el segundo 480.
Ambas propuestas parecen razonables, pero tienen serias objeciones en el razonamiento.
El caballero de Méré: Antoine Gombaud, apodado el caballero de Méré (Basulto Santos y Camúñez, 2007), un intelectual francés del 1600, propuso el problema a Blaise Pascal, quien lo discutió a través de un intercambio epistolar con Pierre de Fermat. Ambos matemáticos razonaron en términos de cuántas formas cada uno de los jugadores puede ganar la partida, proponiendo cada uno un método que resultaron ser equivalentes.
Usando la notación moderna se tendría que:
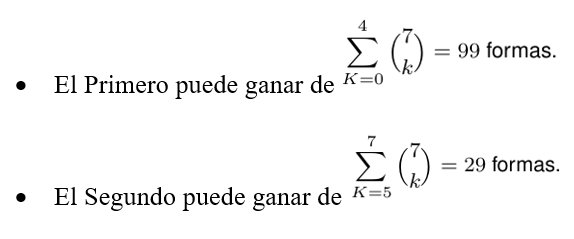
Lo que significa que al primer jugador le corresponderán 928 monedas y al segundo, 272.
El problema también fue abordado por el científico holandés Christiaan Huygens, quien para resolver el problema introdujo un nuevo concepto, el Valor Esperado. Sus estudios fueron incluidos en el libro De Ratiociniis de Ludo Aleae, publicado en 1657. Los avances obtenidos en el cálculo de probabilidad, desde Cardano a Huygens, fueron compilados por el matemático francés Pierre-Simon Laplace (Gutiérrez, 2012) en el texto Théorie analytique des probabilités. Este modelo de probabilidad podría llamarse combinatorio.
6. EL CÁLCULO DEL RIESGO
Pero no fueron solo los juegos de azar los que motivaron el cálculo de probabilidades. Otros problemas, de índole muy distinta, también motivaron su estudio: los problemas actuariales.
El primer contrato de seguro se firmó en 1347, en el puerto de Génova, con el fin de proteger el comercio marítimo. La apertura de nuevas rutas comerciales a partir de 1500 dio un gran impulso a esta actividad, creándose grandes aseguradoras en Francia, España e Inglaterra. Para determinar la póliza del seguro, es necesario medir el riesgo de la actividad, es decir la probabilidad de que la actividad fracase. Este es un problema de naturaleza muy distinta al de los juegos de azar, que pueden reducirse a cálculos combinatorios. ¿Cómo medir la probabilidad en estos casos?
Si existe un registro suficientemente extenso de la actividad marítima y se sabe, por ejemplo, que del total de travesías transcontinentales un 18% de ellas fracasan. Razonablemente se puede asumir que un determinado viaje tendrá una probabilidad de fracaso de 0,18 y de éxito de 0,82. La idea, detrás de este supuesto es que las frecuencias relativas de ocurrencia de cierto fenómeno tienden a la probabilidad de este, es decir: Si A es el resultado de un determinado fenómeno F y an es el número de veces que se ha obtenido el resultado A, en n realizaciones del fenómeno F, entonces:
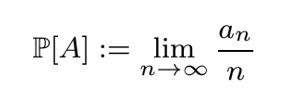
Este enfoque de cálculo de probabilidad es denominado frecuentista y está en la base de la mirada estadística de la probabilidad.
Detrás de esta idea hay varios supuestos implícitos, como por ejemplo que es factible reproducir el fenómeno estudiado un número indeterminado de veces y que la sucesión an /n converge a un límite.
El primero en enunciar la idea fue Cardano, quien sin prueba alguna, enunció que la estadística empírica tiende a mejorar con el número de ensayos. Pero el primero en abordar formalmente este resultado fue Jacob Bernoulli. Le llevó más de veinte años desarrollar una prueba matemática suficientemente rigurosa, que fue publicada en su Ars Conjectandi (El arte de la conjetura) en 1713. Bernoulli sentía un especial afecto por este resultado, al cual llamaba su Teorema Dorado. En 1837, S. D. Poisson describió con más detalle bajo el nombre de la loi des grands nombres (la ley de los grandes números).
No obstante todos estos avances en el cálculo de probabilidades, aún no existía una auténtica Teoría de Probabilidades; es decir, una axiomatización de la probabilidad.
7. AXIOMATIZACIÓN DE KOLMOGOROV
En el proceso de axiomatización de la probabilidad participaron grandes matemáticos, como Chebyshev, Markov, Borel, Cantelli, entre otros. Pero quien logra una axiomatización completa, basada en la Teoría de la Medida y el Análisis Funcional, fue el matemático soviético Kolmogorov, quien en su libro Los Fundamentos de la Teoría de la Probabilidad, publicado 1933, estableció la base moderna de la Teoría de Probabilidades.
Partiendo del esquema de Cardano, donde Ω = {x1, . . . , xn} son los posibles resultados de un fenómeno y la probabilidad de ocurrencia de un evento X ⊂ Ω está dado por
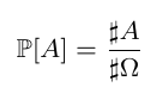
Es muy natural hacerse las siguientes preguntas:
- Dados eventos A y B, ¿cuál es la probabilidad de ocurrencia simultánea de A y B?
- ¿Cuál es la probabilidad de ocurrencia de alguno de ellos?
- ¿Cuál es la probabilidad de que no ocurra A?
- ¿Cuál es la probabilidad de que ocurra A, pero no B?
Las respuestas a estas preguntas requieren de la operaciones clásicas de conjuntos, como unión, intersección y complemento. Es decir, el conjunto potencia de Ω se dota de una estructura de álgebra de conjuntos. Pero esta estructura rápidamente se muestra insuficiente cuando se quiere estudiar fenómenos con una cantidad infinita de resultados, por lo que se deben considerar procesos de unión e intersección infinita de conjuntos. Para esto se requerirá una estructura mucho más completa, la de σ-álgebra.
En la axiomatización de Kolmogorov se parte de un conjunto Ω, al igual que en el esquema de Cardano, pero ahora se podrá admitir que Ω tenga una cantidad infinita de elementos.
Los eventos serán tomados en una familia F de subconjunto de Ω que tenga estructura de σ-álgebra y la probabilidad será una función IP:F→[0,1]. Es decir, un espacio de probabilidad será una terna (Ω, F, IP).
El enorme éxito que ha tenido la Teoría de Probabilidades en la descripción de los más variados fenómenos ha distraído la discusión sobre qué es el azar y que lo produce, pues independiente de la postura filosófica que se pueda adoptar, los experimentos muestran una correspondencia muy precisa entre teoría y realidad. Tan fuerte es esta correspondencia, que pareciera que el tema está totalmente cerrado y se ha llegado al Modelo Final para el azar. Pero la historia aún no termina.
8. MÁS ALLÁ DE KOLMOGOROV
Con el desarrollo de la física cuántica, aparecieron fenómenos con comportamiento totalmente nuevo, que no tienen analogía con la experiencia cotidiana.
• Postulado 1. El Sistema Cuántico: cualquier sistema cuántico aislado tiene asociado un espacio de Hilbert complejo. El sistema se describe totalmente por un estado que es un operador positivo con traza unitaria, actuando sobre el espacio de Hilbert del sistema.
• Postulado 2. Observables y Regla de Bohr: los observables de un sistema cuántico se representan por operadores autoadjuntos, estos tienen una descomposición espectral del tipo:
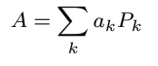
Donde ak son los valores propios del operador A y Pk representa un operador de proyección sobre el espacio propio asociado con el valor propio ak.
Por lo tanto, un Espacio de Probabilidad Cuántico es una dupla (H, ρ) donde H es un espacio de Hilbert Complejo y ρ es operador positivo con traza unitaria.
Tabla 1. Comparación entre el esquema clásico y el cuántico

9. A MODO DE CONCLUSIÓN
Para un determinado fenómeno físico, su probabilidad de ocurrencia puede ser vista como una propiedad de este, como puede ser su temperatura, su masa o su velocidad.
• La teoría de probabilidad, como herramienta humana para comprender los fenómenos aleatorios, va evolucionando junto con el conocimiento humano general.
• Independiente de que creamos que la aleatoriedad es ontológica o epistemológica, las nuevas teorías científicas, como la teoría del caos y la teoría cuántica, nos muestran que seguirá estando presente en nuestra compresión del mundo.
• Como dice Javier Krahe, es preferible caminar con una duda que con un mal axioma (Krahe, J. 1988).
REFERENCIAS BIBLIOGRÁFICAS
Basulto Santos, J. y Camúñez, J. (2007). El problema de los dados del caballero de Méré: soluciones publicadas en el siglo XVII. Suma, 56, 43-54.
Krahe, J, Pérez, A, Sabina, J. (1988). El comosoma. Elígeme. Recuperado de: https://www.youtube.com/watch?v=EAywexXPX04
Museo Caldoval (2022). Dados y fichas de hueso [imagen]. Recuperado de: https://museocaldoval.gal/es/deporte-en-roma/xogos-romanos.
Delmastro, A. L., Vílchez, M. y Villalobos, F. (2004). Wagensberg, el azar y la complejidad: implicaciones y aplicaciones en el ámbito educativo. Agora, 14, 101-119.
Gentile, M. E. (1998). La pichca: oráculo y juego de fortuna (su persistencia en el espacio y tiempo andinos). Bulletin de l’Institut français d’études andines, 27(1).
Gutiérrez, S. (2012). Laplace, matemático del azar. Suma, 71, 87-96.
Rodríguez-Donís, M. (1997). Azar, naturaleza y arte en los atomistas y en Platón. Anuario Filosófico, 30(1).
Rossi, G. (2013). El azar según Aristóteles. Cuadernos de filosofía, 60, 123.
Swezey, W. R. y Bittman, B. (1983). El rectángulo de cintas y el patolli: nueva evidencia de la antigüedad, distribución, variedad y formas de practicar este juego precolombino. Mesoamerica, 4(6), 373-416.
Taboada, C. (2014). Pichcas procedentes de Huaca Tres Palos en Perú [imagen]. Recuperado de: https://www.researchgate.net/figure/Figura-3-1-2-y-3-Pichcas-halladas-en-Santiago-del-Estero-en-Sequia-Vieja-MW-Averias_fig1_281452704.
Vega-Amaya, O. (2002). Surgimiento de la teoría matemática de la probabilidad. Apuntes de historia de las matemáticas, 1(1), 54-62.
Wikipedia (2006). El Zocchiedro [imagen]. Recuperado de: https://es.wikipedia.org/wiki/Zocchiedro